How To Work Out Volume Of Gas From Moles

Using this calculator, you can calculate the molar volume of a gas for arbitrary temperature and pressure. Just note that for big values real gases divert from ideal gas law (that's why they are not "ideal") and this formula can't be used. There are several steps involved in this calculation. First, we must determine the question, which is to calculate the volume of a quantity of gas at a given temperature and pressure. In a second step, after establishing a basis, we must convert the mass of methane that will be the basis into pound moles.

Third, we must convert temperature in degrees Fahrenheit into absolute degrees Rankin and, fourth, convert pressure from psig into psia. Fifth, we must select the appropriate ideal gas constant and use it with a rewritten form of Equation 4.11 to determine the volume of 11.0 lbs of methane gas. Finally, we can substitute the values previously determined into the rewritten equation to calculate the volume.

Eventually, these individual laws were combined into a single equation—the ideal gas law—that relates gas quantities for gases and is quite accurate for low pressures and moderate temperatures. We will consider the key developments in individual relationships , then put them together in the ideal gas law. The behavior of gases can be described by several laws based on experimental observations of their properties. The pressure of a given amount of gas is directly proportional to its absolute temperature, provided that the volume does not change (Amontons's law). The volume of a given gas sample is directly proportional to its absolute temperature at constant pressure (Charles's law).

How To Calculate Volume Of Gas From Moles The volume of a given amount of gas is inversely proportional to its pressure when temperature is held constant (Boyle's law). Under the same conditions of temperature and pressure, equal volumes of all gases contain the same number of molecules (Avogadro's law). Hydrogen gas has the chemical formula H2 and the molecular weight of 2. This gas is the lightest substance among all chemical compounds and the most abundant element in the universe.

Hydrogen gas has also drawn significant attention as a potential energy source. Hydrogen can be obtained, for example, by electrolysis of the water. You calculate the amount of hydrogen in moles either from the gas mass or using the ideal gas law.

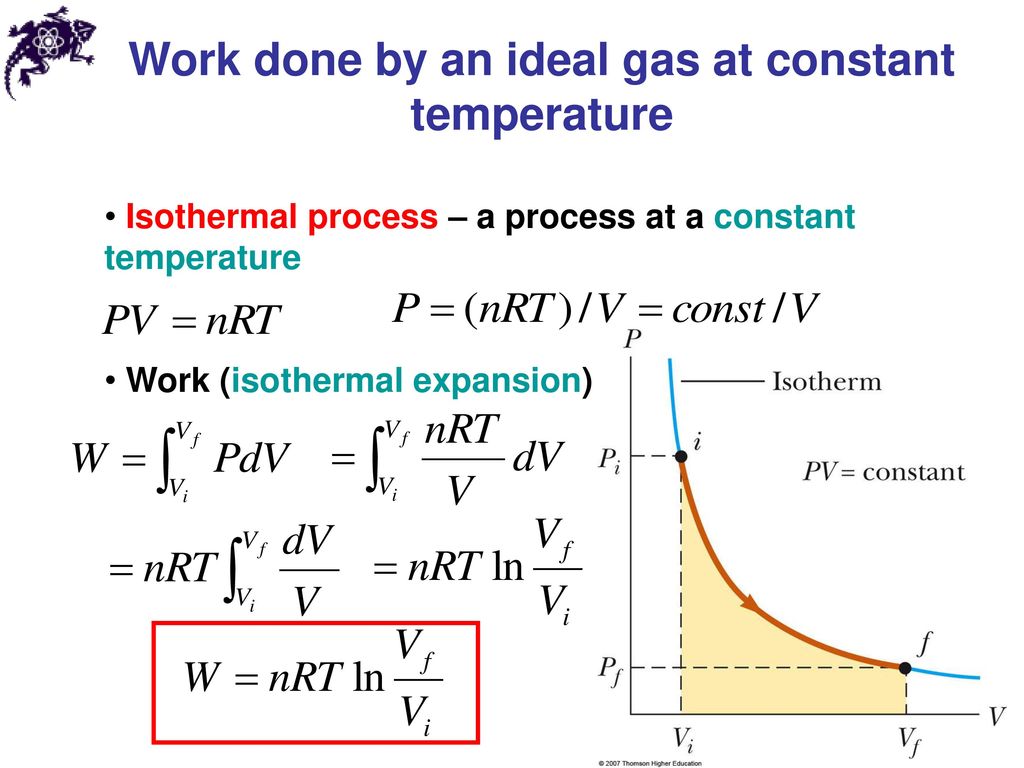
One mole of an ideal gas has a volume of 22.4 L at standard temperature and pressure. And is a proportionality constant that relates the values of pressure, volume, amount, and temperature of a gas sample. The variables in this equation do not have the subscripts i and f to indicate an initial condition and a final condition. The ideal gas law relates the four independent properties of a gas under any conditions. Gases whose properties of P, V, and T are accurately described by the ideal gas law are said to exhibit ideal behavior or to approximate the traits of an ideal gas. An ideal gas is a hypothetical construct that may be used along with kinetic molecular theory to effectively explain the gas laws as will be described in a later module of this chapter.

Although all the calculations presented in this module assume ideal behavior, this assumption is only reasonable for gases under conditions of relatively low pressure and high temperature. In the final module of this chapter, a modified gas law will be introduced that accounts for the non-ideal behavior observed for many gases at relatively high pressures and low temperatures. In grade 10 learners learnt about the molar volume of gases.

This concept is refreshed here and then expanded on to cover any number of moles of gases. The ideal gas law is written for ideal or perfect gases. You can use values for real gases so long as they act like ideal gases.

To use the formula for a real gas, it must be at low pressure and low temperature. Increasing pressure or temperature raises the kinetic energy of the gas and forces the molecules to interact. While the ideal gas law can still offer an approximation under these conditions, it becomes less accurate when molecules are close together and excited. Previously, we considered only ideal gases, those that fit the assumptions of the ideal gas law. Gases, however, are never perfectly in the ideal state.

When pressure is low and temperature is low, gases behave similarly to gases in the ideal state. When pressure and temperature increase, gases deviate farther from the ideal state. We have to assume new standards, and consider new variables to account for these changes. A common equation used to better represent a gas that is not near ideal conditions is the van der Waals equation, seen below. We can then convert these amounts in moles to mass, volume etc. as required.

The ideal gas law formula states that pressure multiplied by volume is equal to moles times the universal gas constant times temperature. To get to moles, use the equation and the molar ratios shown. To get to volume, use the molar volume of gas constants. To get to mass, use the atomic/molecular masses shown in the periodic table. To calculate the concentration in metric dimensions, with other temperature and pressure conditions the Ideal Gas Law comes in handy. The volume divided by the number of molecules represents the molar volume of the gas with a temperature and pressure .

If themolecular massof a gas is known, the ideal gas law can be manipulated to find the density of the gas. It's just a matter of plugging in the right variables and performing a few calculations. This relationship between temperature and pressure is observed for any sample of gas confined to a constant volume. An example of experimental pressure-temperature data is shown for a sample of air under these conditions in Figure 9.11. Where Z is the gas compressibility factor, which is a useful thermodynamic property for modifying the ideal gas law to account for behavior of real gases.

The above equation is basically a simple equation of state . Is the volume occupied by one mole of a chemical element or a chemical compound. It can be calculated by dividing the molar mass by mass density (ρ). Molar gas volume is one mole of any gas at a specific temperature and pressure has a fixed volume. The volume and temperature are linearly related for 1 mole of methane gas at a constant pressure of 1 atm. If the temperature is in kelvin, volume and temperature are directly proportional.

Charles's law states that the volume of a given amount of gas is directly proportional to its temperature on the kelvin scale when the pressure is held constant. Today's more and more there is an interest to express gas concentrations in metric units, i.e. µg/m3. Although expressing gaseous concentrations in µg/m3 units, has the advantage of metric expression, it has the disadvantage of being greatly influenced by changes in temperature and pressure. Additionally, because of difference in molecular weight, comparisons of concentrations of different gases are difficult.

Note one of gas laws state, the same number of moles of any gaseous substance will have the same volume at constant temperature and pressure. So x moles of $\ce$ will hold the same volume as x moles of oxygen gas, so 4.2 litres. We have just seen that the volume of a specified amount of a gas at constant pressure is proportional to the absolute temperature. In addition, we saw that the volume of a specified amount gas at a constant temperature is also inversely proportional to its pressure.

We can correctly assume that pressure of a specified amount of gas at a constant volume is proportional to its absolute temperature. Let us also add the fact that the volume at constant pressure and temperature is also proportional to the amount of gas. Similarly, the pressure at constant volume and temperature is proportional to the amount of gas. Thus, these laws and relationships can be combined to give Equation 4.10.

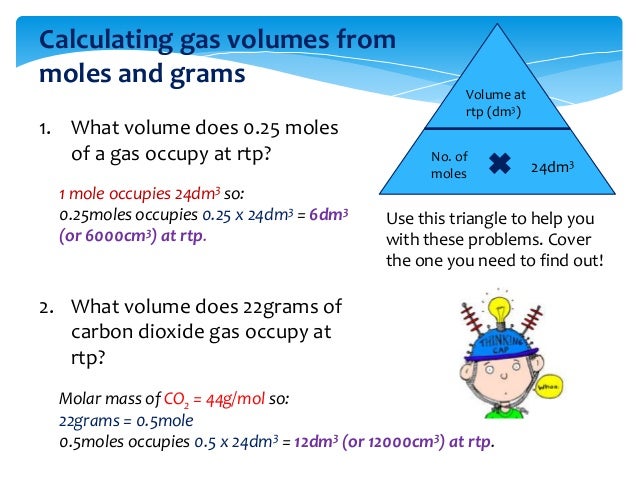
If a sample of gas has an initial pressure of 1.56 atm and an initial volume of 7.02 L, what is the final volume if the pressure is changed to 1,775 torr? Assume that the amount and the temperature of the gas remain constant. Use common sense to calculate the volume of quantities of gas other than one mole. Clearly two moles of gas would occupy 48 dm3, that is 2 × 24. So, in general, multiply the number of moles by 24 to get the volume of gas in dm3 at room temperature and pressure.

The molar volume of gas at STP, standard temperature and pressure (0°C or 273K, 100 kPa pressure) is 22.4 litres per mole (22.4 L/mol). In other words, one mole of atoms of a pure ideal gas at 0°C will fill 22.4 litres of space. The molar volume of gas at room temperature (25°C, 298K) and pressure is 24 litres per mole (24 L/mol).

Examples and practice problems of solving equation stoichiometry questions with gases. We calculate moles with 22.4 L at STP, and use molar mass and mole ratios to figure out how many products or reactants we have. Gases aren't very dense compared to solids and liquids, but they still have a density.

Density is defined as mass per volume, and the relation between mass and moles of course is the molecular weight, Mw. The reader may have noticed that in the examples above, we really didn't care which ideal gas we talked about, just that it was ideal. Usually with density calculations, we need to know what gas we are talking about so we can calculate its molecular weight and thus put mass into the calculation. The volume-volume problems are the easiest since according to the Law of Combining Gas Volumes, gases combine at the same temperature and pressure in simple whole number of volumes.

One mole of any gas occupies the same volume when measured under the same conditions of temperature and pressure. In this experiment, the volume of one mole of hydrogen is calculated at room temperature and pressure. To apply this gas law, the amount of gas should remain constant. As with the other gas laws, the temperature must be expressed in kelvins, and the units on the similar quantities should be the same.

Because of the dependence on three quantities at the same time, it is difficult to tell in advance what will happen to one property of a gas sample as two other properties change. The best way to know is to work it out mathematically. If a sample of gas has an initial pressure of 375 torr and an initial volume of 7.02 L, what is the final pressure if the volume is changed to 4,577 mL?

Assume that amount and the temperature of the gas remain constant. It is possible to calculate the volume of one mole of gas at standard temperature and pressure using what we now know about gases. At the end of the chapter learners bring together all the concepts that they have learnt into this topic.

Learners are introduced to the idea that the balanced chemical equation can be used to calculate any quantity of a substance from any of the other products or reactions in that reaction. According to the stoichiometry of the equation, 4 mole of e- are required to produce 2 moles of hydrogen gas, or 2 moles of e-'s for every one mole of hydrogen gas. I want to repeat the example I used when we were talking about calculations from equations using masses, but this time calculate the volume of carbon dioxide produced.

The interest stems from that accurate measurements of the unit cell volume, atomic weight and mass density of a pure crystalline solid provide a direct determination of the Avogadro constant. The ideal gas equation contains five terms, the gas constant R and the variable properties P, V, n, and T. Specifying any four of these terms will permit use of the ideal gas law to calculate the fifth term as demonstrated in the following example exercises. A small teaspoon of sodium hydrogencarbonate weighs 4.2g. Calculate the moles, mass and volume of carbon dioxide formed when it is thermally decomposed in the oven.

Assume room temperature for the purpose of the calculation. The most common molar volume is the molar volume of an ideal gas at standard temperature and pressure (273 K and 1.00 atm). Read on to find out more about the ideal gas law, moles, and examples & tips on how to resolve chemical equations. Multiply the volume and pressure and divide the product by the temperature and the molar gas constant to calculate moles of the hydrogen gas. This relationship shows us that if we increase the moles of gas, n, by adding more gas while maintaining the same temperature and pressure, the volume of gas, V, will also increase. This means equal amounts of moles of gases occupy the same volume under the same conditions of temperature and pressure.

1 mole of any gas at STP occupies 22.4 liters of volume. Using this information, the volume occupied by any number of moles can be determined. Conversely, the number of moles present in any volume of gas at STP can also be determined, and if the identity of the gas is known, this number of moles can be converted to a mass. Since $\ce$ is in excess, the amount of $\ce$ produced will be twice as the amount of moles of oxygen.

So if there is originally x moles of oxygen gas, 2x moles of $\ce$ is produced. It is important to note that temperature and pressure remain constant throughout the reaction. As we stated earlier, the shape of a gas is determined entirely by the container in which the gas is held. Sometimes, however, the container may have small holes, or leaks. Molecules will flow out of these leaks, in a process called effusion.

Because massive molecules travel slower than lighter molecules, the rate of effusion is specific to each particular gas. We use Graham's law to represent the relationship between rates of effusion for two different molecules. This relationship is equal to the square-root of the inverse of the molecular masses of the two substances.

This online calculator calculates the molar volume of an ideal gas at different conditions . You can read about the formula and the most commonly used conditions below the calculator. If the conditions are not at STP, a molar volume of 22.4 L/mol is not applicable. However, if the conditions are not at STP, the combined gas law can be used to calculate the volume of the gas at STP; then the 22.4 L/mol molar volume can be used.